Montgomery 乗算を実装した
modulo 演算の高速化です。
これらのうち、Montgomery 乗算というものを実装しました。
余談? 経緯?
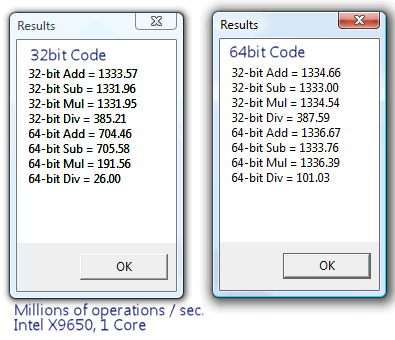
Codeforces では C++ 以外 32bit 環境なんだよなとふと思って、演算にどれだけの差が出るのか調べてみました。
どうやら 32bit 環境での 64bit 整数同士の乗算・除算は特に遅いらしい。
Montgomery 乗算とは
中国剰余定理の応用みたいなもので、例えば奇数 $M$ に対して、$\bmod M$ の演算を「% M」の代わりに $2$ の冪による除算・剰余算(bit 演算)で済ませることができます。$M < 2^{31} = 2147483648$ なら 32bit 整数でうまい感じにできます。
こちらを参考にしました。これらが完璧すぎるので自分は書くことがありません。
というか「modulo 演算の速度差が問題になるようなコンテストに出ない!(素振り)」案件なんですよね。AtCoder や Library Checker では有意な差すら確認できていないのですが(ベンチマークになる問題があれば教えてください)、Codeforces で NTT を投げてみたらこんなことがあり
Submission #97560132 - Codeforces TLE (>4000 ms)
Submission #97563421 - Codeforces AC (2262 ms)
main 関数の中身は同じです。さすがにおかしくないか? 32bit だと $2^{30}$ 程度の定数による除算・剰余算があまり最適化されなかったりするんでしょうか。
実装
yukicoder Wiki、Wikipedia の内容をそのまま実装します。法は奇数であればよいですが、素数と仮定することにします。
せっかくこういうことをするのに ACL の dynamic_modint みたいなのを提供しないのはもったいないんですが、Mod の値を const にしたいので切りました。